Bijection

A bijection (or bijective function or one-to-one correspondence) is a function giving an exact pairing of the elements of two sets. Every element of one set is paired with exactly one element of the other set, and every element of the other set is paired with exactly one element of the first set. (There are no unpaired elements.)

A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements. For infinite sets the picture is more complex, leading to the concept of cardinal number, a way to distinguish the various sizes of infinite sets.

A bijective function from a set to itself is also called a permutation.

Bijective functions are essential to many areas of mathematics including the definitions of isomorphism, homeomorphism, diffeomorphism, permutation group, and projective map.

1 Definition
2 Example
3 Inverses
4 Composition
5 Bijections and cardinality
6 Examples and non-examples
7 Properties
8 Bijections and category theory
9 See also
10 Notes
11 References
12 External links

Definition

To have an exact pairing between X and Y (where Y need not be different from X), four properties must hold:

each element of X must be paired with at least one element of Y,
no element of X may be paired with more than one element of Y,
each element of Y must be paired with at least one element of X, and
no element of Y may be paired with more than one element of X.

Satisfying properties (1) and (2) means that a bijection is a function with domain X. It is more common to see properties (1) and (2) written as a single statement: Every element of X is paired with exactly one element of Y. Functions which satisfy property (3) are said to be "onto Y " and are called surjections (or surjective functions). Functions which satisfy property (4) are said to be "one-to-one functions" and are called injections (or injective functions).^[1] With this terminology, a bijection is a function which is both a surjection and an injection, or using other words, a bijection is a function which is both one-to-one and onto.

Example

As a concrete example of a bijection, consider the batting line-up of a baseball team. The set X will be the nine players on the team and the set Y will be the nine positions in the batting order (1^st, 2^nd, 3^rd, etc.) The "pairing" is given by which player is in what position in this order. Property (1) is satisfied since each player is somewhere in the list. Property (2) is satisfied since no player bats in two (or more) positions in the order. Property (3) says that for each position in the order, there is some player batting in that position and property (4) states that two or more players are never batting in the same position in the list.

Inverses

A bijection f with domain X ("functionally" indicated by f: X → Y) also defines a relation starting in Y and going to X (by turning the arrows around). The process of "turning the arrows around" for an arbitrary function does not usually yield a function, but properties (3) and (4) of a bijection say that this inverse relation is a function with domain Y. Moreover, properties (1) and (2) then say that this inverse function is a surjection and an injection, that is, the inverse function exists and is also a bijection. Functions that have inverse functions are said to be invertible. Bijections are the invertible functions.

Stated in concise mathematical notation, a function 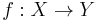$f:X \rightarrow Y$ is bijective if and only if it satisfies the condition

for every 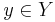$y \in Y$ there is a unique 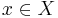$x\in X$ with $y=f(x)$ .

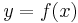Continuing with the baseball batting line-up example, the function that is being defined takes as input the name of one of the players and outputs the position of that player in the batting order. Since this function is a bijection, it has an inverse function which takes as input a position in the batting order and outputs the player who will be batting in that position.

Composition

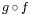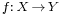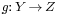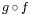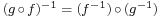The composition $\scriptstyle g \,\circ\, f$ of two bijections $\scriptstyle f:\,X \,\to\, Y$ and $\scriptstyle g:\, Y \,\to\, Z$ is a bijection. The inverse of $\scriptstyle g \,\circ\, f$ is $\scriptstyle (g \,\circ\, f)^{-1} \;=\; (f^{-1}) \,\circ\, (g^{-1})$ .

Conversely, if the composition 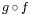$\scriptstyle g \,\circ\, f$ of two functions is bijective, we can only say that f is injective and g is surjective.

Bijections and cardinality

The definition of a number If X and Y are finite sets, then there exists a bijection between the two sets X and Y if and only if X and Y have the same number of elements. Indeed, in axiomatic set theory, this is taken as the definition of "same number of elements", and generalising this definition to infinite sets leads to the concept of cardinal number, a way to distinguish the various sizes of infinite sets.

Examples and non-examples

For any set X, the identity function 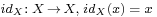$\scriptstyle id_X:\; X \,\rightarrow\, X,\; id_X(x) \;=\; x$ , is bijective.
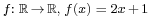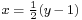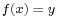The function $\scriptstyle f:\; \R \,\rightarrow\, \R,\; f(x) \;=\; 2x \,%2B\, 1$ is bijective, since for each y there is a unique $\scriptstyle x \;=\; \frac{1}{2}\left(y \,-\, 1\right)$ such that $\scriptstyle f(x) \;=\; y$ .
The exponential function, 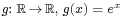$\scriptstyle g:\; \R \,\rightarrow\, \R,\; g(x) \;=\; e^x$ , is not bijective: for instance, there is no $\scriptstyle x \,\in\, \R$ such that 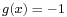$\scriptstyle g(x) \;=\; -1$ , showing that g is not surjective. However if the codomain is restricted to the positive real numbers 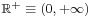$\scriptstyle \R^%2B \;\equiv\; \left(0,\, %2B\infty\right)$ , then g becomes bijective; its inverse is the natural logarithm function ln.
The function 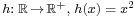$\scriptstyle h:\; \R \,\rightarrow\, \R^%2B,\; h(x) \;=\; x^2$ is not bijective: for instance, 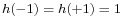$\scriptstyle h(-1) \;=\; h(%2B1) \;=\; 1$ , showing that h is not injective. However, if the domain is restricted to 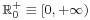$\scriptstyle\R^%2B_0 \;\equiv\; \left[0,\, %2B\infty\right)$ , then h becomes bijective; its inverse is the positive square root function.

Properties

A function 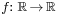$\scriptstyle f:\; \R \,\rightarrow\, \R$ is bijective if and only if its graph meets every horizontal and vertical line exactly once.
If X is a set, then the bijective functions from X to itself, together with the operation of functional composition (∘), form a group, the symmetric group of X, which is denoted variously by S(X), S_X, or X! (X factorial).
Bijections preserve cardinalities of sets: for a subset A of the domain with cardinality |A| and subset B of the codomain with cardinality |B|, one has the following equalities:

|f(A)| = |A| and |f⁻¹(B)| = |B|.
If X and Y are finite sets with the same cardinality, and 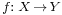, then the following are equivalent:
1. f is a bijection.
2. f is a surjection.
3. f is an injection.
For a finite set S, there is a bijection between the set of possible total orderings of the elements and the set of bijections from S to S. That is to say, the number of permutations of elements of S is the same as the number of total orderings of that set—namely, n!.

Bijections and category theory

Bijections are precisely the isomorphisms in the category Set of sets and set functions. However, the bijections are not always the isomorphisms for more complex categories. For example, in the category Gr of groups, the morphisms must be homomorphisms since they must preserve the group structure, so the isomorphisms are group isomorphisms which are bijective homomorphisms.

Notes

^ There are names associated to properties (1) and (2) as well. A relation which satisfies property (1) is called a total relation and a relation satisfying (2) is a single valued relation.

References

This topic is a basic concept in set theory and can be found in any text which includes an introduction to set theory. Almost all texts that deal with an introduction to writing proofs will include a section on set theory, so the topic may be found in any of these:

Wolf (1998). Proof, Logic and Conjecture: A Mathematician's Toolbox. Freeman.
Sundstrom (2003). Mathematical Reasoning: Writing and Proof. Prentice-Hall.
Smith; Eggen; St.Andre (2006). A Transition to Advanced Mathematics (6th Ed.). Thomson (Brooks/Cole).
Schumacher (1996). Chapter Zero: Fundamental Notions of Abstract Mathematics. Addison-Wesley.
O'Leary (2003). The Structure of Proof: With Logic and Set Theory. Prentice-Hall.
Morash. Bridge to Abstract Mathematics. Random House.
Maddox (2002). Mathematical Thinking and Writing. Harcourt/ Academic Press.
Lay (2001). Analysis with an introduction to proof. Prentice Hall.
Gilbert; Vanstone (2005). An Introduction to Mathematical Thinking. Pearson Prentice-Hall.
Fletcher; Patty. Foundations of Higher Mathematics. PWS-Kent.
Iglewicz; Stoyle. An Introduction to Mathematical Reasoning. MacMillan.
Devlin, Keith (2004). Sets, Functions, and Logic: An Intoduction to Abstract Mathematics. Chapman & Hall/ CRC Press.
D'Angelo; West (2000). Mathematical Thinking: Problem Solving and Proofs. Prentice Hall.
Cupillari. The Nuts and Bolts of Proofs. Wadsworth.
Bond. Introduction to Abstract Mathematics. Brooks/Cole.
Barnier; Feldman (2000). Introduction to Advanced Mathematics. Prentice Hall.
Ash. A Primer of Abstract Mathematics. MAA.

External links

Weisstein, Eric W., "Bijection" from MathWorld.

Earliest Uses of Some of the Words of Mathematics: entry on Injection, Surjection and Bijection has the history of Injection and related terms.